AI 狂想曲:10亿+高质量题库引爆“数据燃料”革命
AI 如何颠覆循证科学领域?
医生用 AI 筛查三万份病理报告,过去需要三个团队耗时半年的工作,现在系统72小时就能完成初筛。
当训练数据存在个别误差时,再精妙的算法诊断准确率都会断崖式下跌。在循证科学领域,AI 不是替代人类智慧的“魔法黑箱”,而是放大专业价值的“共振器”。它正以三种方式重塑科研范式:
- 让沉默数据开口:未被结构化的数据记录,正通过 NLP 技术转化为可追溯的证据链;
- 让偶然发现可复现:通过知识图谱技术,散落在不同研究中的"边缘结论"开始产生化学反应;
- 让验证周期进化:传统需要数年的双盲实验,现在借助数字孪生技术可完成初步效果推演。
但所有这些变革都建立在同一个地基之上:经得起实证考验的高质量数据。我们现在正处在拐点中——当大模型推理能力逐渐突破小学数学、初中数学、高中数学、乃至高等数学,背后是每一条推理训练数据都经历数十次数学求解校验的结果。
也许不久的将来,评价科研机构实力的指标不再是发了多少顶刊,而是储备了多少高质量“数据燃料”。在 AI 狂飙时代,数据不再是研究的副产品,而是生产的干细胞。当您准备构建自己的 AI 推理验证系统时,不妨先问问:我的数据题库,经得起多少次双重盲审?
如何构建对大模型有帮助的高质量数据?
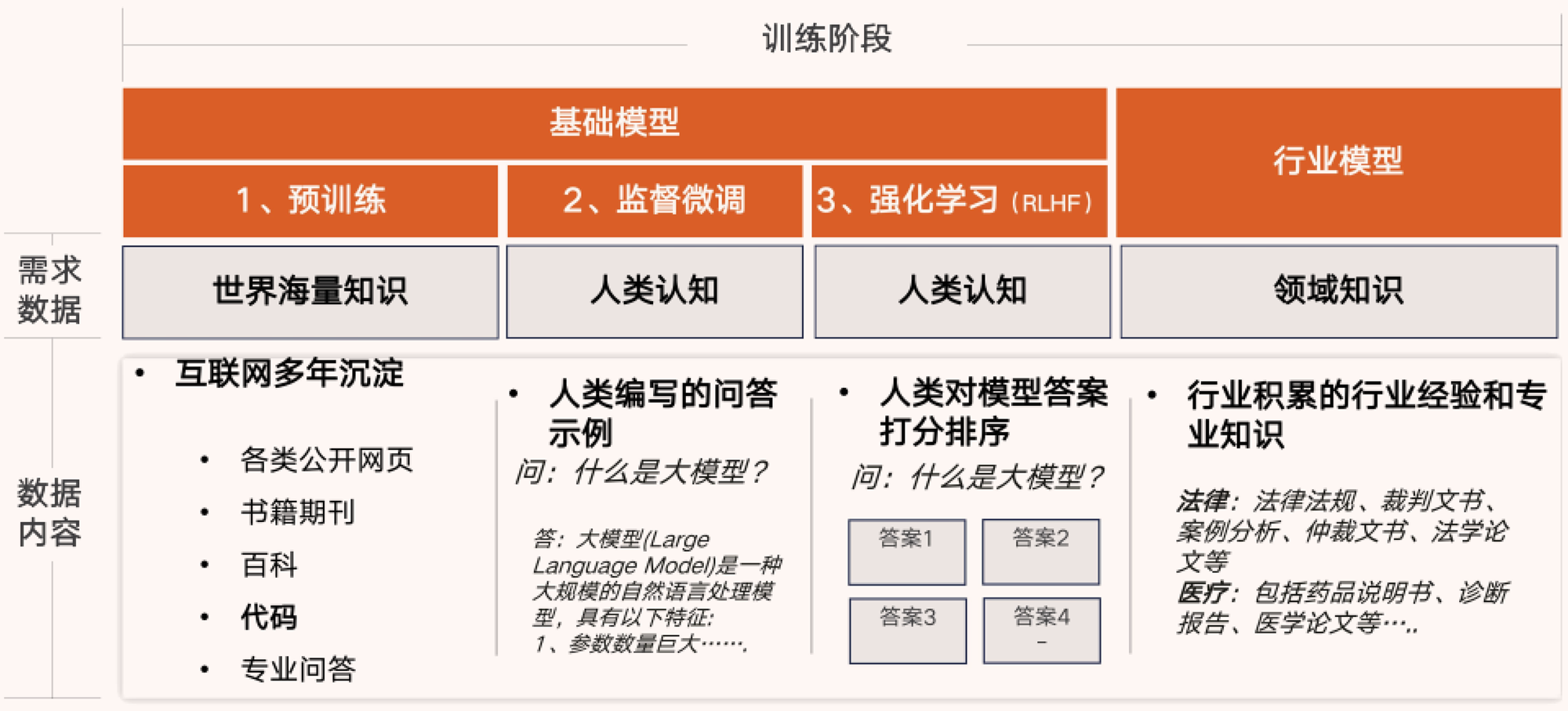
大模型成长之路
大模型所需要的数据根据训练的阶段有所不同。以 ChatGPT 为代表的大语言模型(LLM)为例,其训练过程分为预训练(Pre-training)、监督微调(SFT)、基于人类反馈的强化学习(RLHF)三个阶段。
- 第一阶段预训练所需的语料是各种类型的世界知识,通过大量学习世界知识,构建模型的基础能力,理解客观世界的规律;
- 第二阶段 SFT,通过标注人员设计问答,编写正确答案,将例题投喂给模型,并希望模型在没有见过的任务中“举一反三”,提升泛化能力;
- 第三阶段 RLHF,训练目标是让模型的价值观与人类对齐,让模型知道“怎么说更好”。
高质量数据的重要性
由于高质量数据可以更好地模拟客观世界,将其作为训练数据可以增强模型能力。从模型能力表现看:
- 高质量数据可以提升模型的 准确性和稳定性。这些数据通常包含更准确和丰富的信息,有助于模型更好地理解数据的内在结构,提升产出的精准性。其次,高质量的数据清洗 Pipeline 是提高数据质量的重要环节,包括去重、删除个人隐私内容、纠正错误、填补缺失值等,经过清洗的数据可以提升训练阶段的稳定性;
- 高质量数据具有多样性,可以降低模型对特定数据集的依赖,提升 鲁棒性和泛化能力。高质量数据通过对现有不同来源的数据加以混合,调试配比,提升模型执行下游任务的泛化能力。同时,数据增强等手段可有效提升多样性,即通过对现有数据进行变换或扩充,生成更多的训练样本,增加训练数据代表性和多样性;
- 为了获取可以用于训练的高质量问答对(QA对)数据,我们采集了大量的问题,并进行人工标注校验。题库数据主要来源于教材与习题册,从中提取出题目文本、答案、知识点信息等,并将其统一存储为 Json 格式。
高质量数据的构建之路
为了提高题库数据集的质量,我们需要三重“筛子”:
- 第一重:我们构建了一整套 Pipeline,对所有题目逐道进行清洗及质量把控
- 从题干入手,判断是否完整,判断是否符合逻辑,进而推出答案是否正确;
- 去除重复数据,处理缺失值,例如删除缺失严重的样本或用插值法填补;
- 检测并处理异常值,确保数据的准确性和一致性。
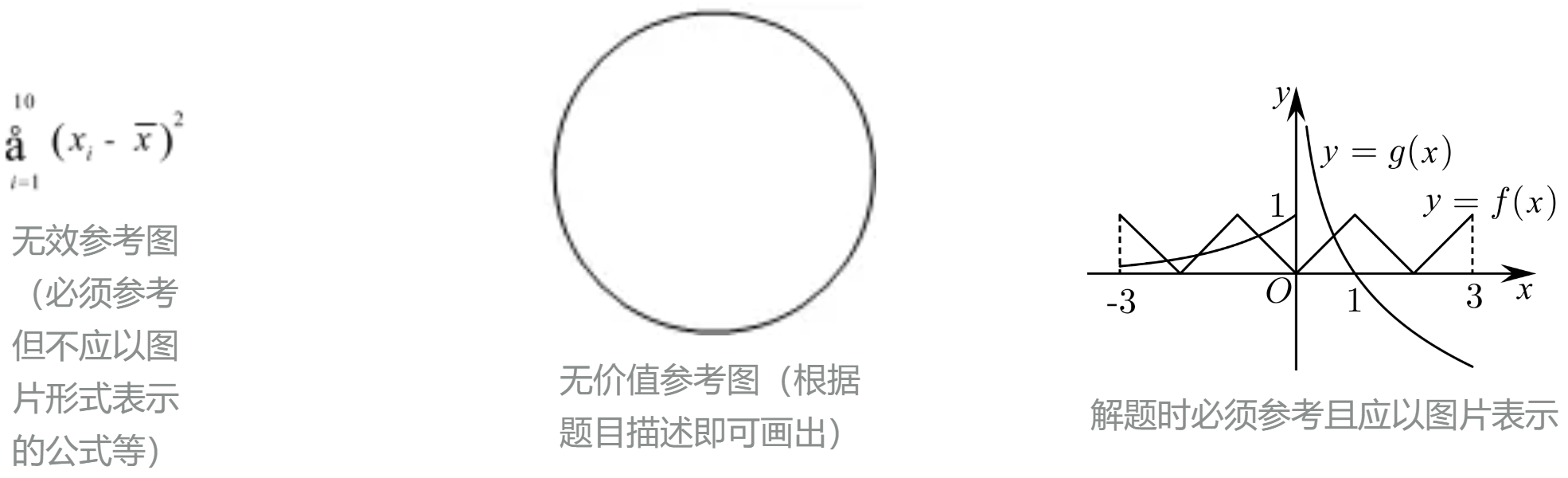
- 第二重:我们对多模态相关题库数据进行专门的处理
- 检测匹配对应题目的图片,确保图片是求解题目必须参考且应以图片表示的,而非将题干或答案解析直接截图的图片。
- 第三重:相应学科领域专家检查
- 对于 K12 阶段习题,我们以学校为单位,请各学段对应学科资深教师进行质量检查;
- 对于大学阶段,我们请相应专业博士生进行质量检查;
- 对于更高深的顶尖领域,我们请相应领域教授团队进行质量检查。
整数打造10亿量级高质量题库数据集,助力大模型发展
为什么大模型训练总是不尽如人意?甚至出现即便违规使用 Benchmark 直接训练后,再用原题考试作答依然不能取得满分的情况?
因为 SFT 阶段对数据质量要求较高,需要来自人类的高质量反馈:通过标注人员设计问答,编写正确答案,将例题投喂给模型,并希望模型在没有见过的任务中“举一反三”,提升泛化能力。由此,对于题库数据集建设的复杂流程,需要投入大量的人力物力,项目周期常常达到数月乃至数年以上。
为此,整数智能推出经过数年积累、剔除低质量题目、人工专家多轮交叉抽检核验,从数十亿的题库、教材、习题册、教师编写团队等处凝练制作出的 10亿+道 全量高质量题库数据集。旨在帮助企业以更低成本、更短周期,满足大模型训练阶段对高质量问答数据的需求。整数智能提供题库数据集具有 多样性、真实性、准确性、定制化 四大优势。
{"id": "f2e4e9c0c97367cb4600b6ae", "title": "设函数$f$在闭区间$[a,b]$上连续,并且$\\int_a^b fdx = 0$。如果对于任意$x\\in [a,b]$,都有$f\\geq 0$,证明:对所有$x \\in [a, b]$有$f=0$。", "option": null, "answer": "利用反证法结合连续函数的介值定理和积分性质进行证明。", "parse": "假设存在$x_0\\in[a,b]$使得$f(x_0)>0$。根据连续函数的局部保号性,在$x_0$附近存在一个小区间$(x_0-\\delta,x_0+\\delta)$(适当缩小以保证仍在$[a,b]$内),在这个小区间内$f>0$。那么$\\int_a^b fdx\\geq\\int_{x_0-\\delta}^{x_0+\\delta}fdx>0$,这与已知条件$\\int_a^b fdx = 0$矛盾。所以对所有$x \\in [a, b]$有$f=0$。", "qtype": "证明题", "subject": "数学/数学分析", "grade": "大学", "has_img": false, "image_analysis": {"img0": {"image_present": false}}, "classification": {"major_category": "Science", "sub_category": "Mathematics", "subject": "Math. Anal."}, "correctness": {"is_correct": true}, "difficulty": {"knowledge_point": "Definite integral, Properties of continuous functions, Intermediate Value Theorem, Proof by contradiction", "knowledge_level": "high school", "educational_stage": "university"}, "quality": {"logical_coherence": 4, "educational_value": 4, "clarity": 4}, "question_metadata": {"question_type": "Short Answer", "language": "Chinese", "ai_generation_likelihood": 4}}
{"id": "dcb705347f19e67c20de8a97", "title": "已知某金属离子$M^{n+}$与氨水反应形成配合物$[M(NH_3)_6]^{n+}$。若该配合物的磁矩为零,且金属离子的电子排布为$d^6$,试确定该金属离子在周期表中的位置,并说明理由。", "option": null, "answer": "铁", "parse": "根据题目信息,金属离子的电子排布为$d^6$,并且形成的配合物磁矩为零,这意味着所有未成对电子都已配对。对于$d^6$电子排布,在八面体场中只有当形成低自旋态时,即所有电子都进入$t_{2g}$轨道并完全配对时,磁矩才会为零。因此,该金属离子应处于第VIII族,常见$d^6$电子排布且能形成低自旋态的金属离子是铁。铁在周期表中的位置为第四周期,第VIII族。", "qtype": "简答题", "subject": "化学/化学", "grade": "大学", "has_img": false, "image_analysis": {"img0": {"image_present": false}}, "classification": {"major_category": "Science", "sub_category": "Chemistry", "subject": "Inorg. Chem."}, "correctness": {"is_correct": true}, "difficulty": {"knowledge_point": "Coordination chemistry, Crystal field theory, Electronic configuration, Magnetic moment, Periodic table", "knowledge_level": "high school", "educational_stage": "university"}, "quality": {"logical_coherence": 4, "educational_value": 4, "clarity": 4}, "question_metadata": {"question_type": "Short Answer", "language": "Chinese", "ai_generation_likelihood": 4}}
{"id": "6aef2e4e9002c2467cb7daeb", "title": "设$D$是由$x=0, y=0, x+y=2$所围成的三角形闭区域,计算二重积分\n$$\nI = \\iint_D (x^2 + y^2) dxdy.\n$$", "option": null, "answer": "$\\frac{8}{3}$", "parse": "首先确定积分区域$D$为由$x=0, y=0, x+y=2$所围成的三角形。选择先对$y$后对$x$积分,则$x$的范围是从$0$到$2$,对于固定的$x$,$y$的范围是从$0$到$2-x$。\n\n\n$$\nI = \\int_0^2 dx \\int_0^{2-x} (x^2 + y^2) dy\n$$\n\n$$\n\\int_0^{2-x} (x^2 + y^2) dy = [x^2y + \\frac{1}{3}y^3]_0^{2-x} = x^2(2-x) + \\frac{1}{3}(2-x)^3\n$$\n\n$$\nI = \\int_0^2 [x^2(2-x) + \\frac{1}{3}(2-x)^3] dx\n$$\n将上式展开并逐项积分可得结果为$\\frac{8}{3}$。", "qtype": "计算题", "subject": "数学/高等数学", "grade": "大学", "has_img": false, "image_analysis": {"img0": {"image_present": false}}, "classification": {"major_category": "Science", "sub_category": "Mathematics", "subject": "Math. Anal."}, "correctness": {"is_correct": true}, "difficulty": {"knowledge_point": "double integral, iterated integral, region of integration, polynomial integration", "knowledge_level": "high school", "educational_stage": "university"}, "quality": {"logical_coherence": 4, "educational_value": 4, "clarity": 4}, "question_metadata": {"question_type": "Calculation", "language": "Chinese", "ai_generation_likelihood": 4}}
{"id": "6aef2e4e97f67cb12d7b4b45", "title": "求解以下初值问题:\n$$ y'' - 5y' + 6y = e^{2t}, \\quad y(0) = 1, \\quad y'(0) = 0 $$", "option": null, "answer": "$y = 3e^{2t} - 2e^{3t} + te^{2t}$", "parse": "\n首先求解对应的齐次方程 $y'' - 5y' + 6y = 0$ 的通解。特征方程为 $r^2 - 5r + 6 = 0$,解得 $r_1 = 2$ 和 $r_2 = 3$。因此齐次方程的通解为 $y_h = C_1e^{2t} + C_2e^{3t}$。\n接下来使用待定系数法求特解。由于非齐次项为 $e^{2t}$,设特解形式为 $y_p = Ate^{2t}$。代入原方程得到 $A = 1$,因此特解为 $y_p = te^{2t}$。\n方程的通解为 $y = y_h + y_p = C_1e^{2t} + C_2e^{3t} + te^{2t}$。\n利用初始条件 $y(0) = 1$ 和 $y'(0) = 0$ 确定常数 $C_1$ 和 $C_2$。由 $y(0) = 1$ 得到 $C_1 + C_2 = 1$;由 $y'(0) = 0$ 得到 $2C_1 + 3C_2 + 1 = 0$。解此线性方程组得到 $C_1 = 3$ 和 $C_2 = -2$。\n因此最终解为 $y = 3e^{2t} - 2e^{3t} + te^{2t}$。", "qtype": "计算题", "subject": "数学/常微分方程", "grade": "大学", "has_img": false, "image_analysis": {"img0": {"image_present": false}}, "classification": {"major_category": "Science", "sub_category": "Mathematics", "subject": "Ord. Diff. Eq."}, "correctness": {"is_correct": true}, "difficulty": {"knowledge_point": "Second-order linear ordinary differential equation, Homogeneous equation, Characteristic equation, Method of undetermined coefficients, Initial value problem, Linear system of equations", "knowledge_level": "high school", "educational_stage": "university"}, "quality": {"logical_coherence": 5, "educational_value": 4.5, "clarity": 5}, "question_metadata": {"question_type": "Calculation", "language": "Chinese", "ai_generation_likelihood": 4}}
{"id": "b3b42b6ae67cf2e4e9b3c866", "title": "设$R=\\mathbb{Z}[x]$,理想$I=(3,x^2+x+1)$。求商环$R/I$中元素的个数。", "option": null, "answer": "9", "parse": "首先注意到$\\mathbb{Z}[x]/(3,x^2+x+1)$可以看作先对$x^2+x+1$取模,再对3取模的结果。由于$x^2+x+1$在$\\mathbb{Z}_3[x]$中是不可约多项式(没有根),因此$\\mathbb{Z}_3[x]/(x^2+x+1)$是一个有9个元素的有限域,即每个元素都可以表示为$a+bx+(x^2+x+1)$的形式,其中$a,b\\in\\mathbb{Z}_3$,共有$3\\times3=9$种组合。", "qtype": "计算题", "subject": "数学/抽象代数", "grade": "大学", "has_img": false, "image_analysis": {"img0": {"image_present": false}}, "classification": {"major_category": "Science", "sub_category": "Mathematics", "subject": "Adv. Algebra"}, "correctness": {"is_correct": true}, "difficulty": {"knowledge_point": "Ideal, Quotient Ring, Finite Field, Irreducible Polynomial, Modular Arithmetic", "knowledge_level": "high school", "educational_stage": "university"}, "quality": {"logical_coherence": 4, "educational_value": 4, "clarity": 4}, "question_metadata": {"question_type": "Calculation", "language": "Chinese", "ai_generation_likelihood": 4}}
【多样性】各学科、教育阶段、难度层次全面覆盖
- K12 校内习题,总量超过 6亿;包括数学、语文、英语、物理、化学、生物、地理等全部学科;覆盖从小学到高中等各阶段年级;支持中文、英文、法文、日文、西班牙文等多种小语种语言。
- 本科及以上校内习题,总量超过 4.5亿,其中理工类学科超过 3.5亿;支持中文、英文、俄文、法文、日文等多种小语种语言。
- 高难度竞赛题库,总量超过 100万 题;包括数学、计算机、物理、化学、生物五大理工竞赛学科;覆盖 K12 和本科各教育阶段;支持中文、英文、俄文、法文、西班牙文等多种小语种语言。
{
"id": "9c0c9330b6ae736f2e4e7cb46",
"title": "Дано $$P(-5,0)$$, точка $$Q$$ лежит на окружности $$(x-5)^{2}+y^{2}=36$$, $$M$$ — середина отрезка $$PQ$$. $$($$Ⅰ$$)$$ Найдите уравнение траектории $$C$$ точки $$M$$. $$($$Ⅱ$$)$$ Прямая $$l$$, проходящая через точку $$P$$, пересекает траекторию $$C$$ в двух точках $$A$$ и $$B$$ ($$A$$ и $$B$$ не совпадают$$)$$. $$①$$ Если $$|AB|=4$$, найдите уравнение прямой $$l$$. $$②$$ Найдите значение $$ \\overrightarrow{PA}⋅ \\overrightarrow{PB}$$.",
"option": null,
"answer": "(Ⅰ) Используя формулу координат середины отрезка и тот факт, что точка Q лежит на заданной окружности, найти уравнение траектории точки M. (Ⅱ) ① Записать уравнение прямой, проходящей через точку P, решить систему уравнений прямой и траектории C. Используя теорему Виета и формулу длины хорды, найти уравнение прямой l. ② Вычислить скалярное произведение векторов, используя их координаты и теорему Виета, чтобы найти его значение.",
"parse": "$$($$Ⅰ$$)$$ Решение: Пусть $$M(x,y)$$, тогда точка, симметричная $$P(-5,0)$$ относительно $$M$$, есть $$Q(2x+5,2y)$$. $$∵$$ Точка $$Q$$ лежит на окружности $$(x-5)^{2}+y^{2}=36$$, $$∴(2x+5-5)^{2}+(2y)^{2}=36$$, то есть $$x^{2}+y^{2}=9$$. Следовательно, уравнение траектории $$C$$ есть $$x^{2}+y^{2}=9$$.\n\n$$($$Ⅱ$$)$$\n①$$ Решение: Пусть $$A(x_{1},y_{1})$$ , $$B(x_{2},y_{2})$$. По условию, угловой коэффициент прямой $$l$$ существует, обозначим его через $$k$$, тогда уравнение прямой $$l$$ есть $$y=k(x+5)$$. Из системы уравнений $$ \\begin{cases} y=k(x+5) \\\\ x^{2}+y^{2}=9\\end{cases}$$, получаем $$(1+k^{2})x^{2}+10k^{2}x+25k^{2}-9=0$$. Из $$ \\triangle =(10k^{2})^{2}-4(1+k^{2})(25k^{2}-9) > 0$$, получаем $$- \\dfrac {3}{4} < k < \\dfrac {3}{4}$$ $$∴x_{1}+x_{2}=- \\dfrac {10k^{2}}{1+k^{2}},x_{1}x_{2}= \\dfrac {25k^{2}-9}{1+k^{2}}$$. $$∵|AB|=4$$, $$∴ \\sqrt {1+k^{2}}|x_{1}-x_{2}|=4$$, $$∴ \\sqrt {1+k^{2}}\\cdot \\sqrt {(x_{1}+x_{2})^{2}-4x_{1}x_{2}}=4$$, $$∴ \\sqrt {1+k^{2}}\\cdot \\sqrt {(- \\dfrac {10k^{2}}{1+k^{2}})^{2}- \\dfrac {4(25k^{2}-9)}{1+k^{2}}}=4$$. Решая, находим $$k=± \\dfrac {1}{2}$$. $$∴$$ Уравнение прямой $$l$$ есть $$y=± \\dfrac {1}{2}(x+5)$$, то есть $$x+2y+5=0$$ или $$x-2y+5=0$$.\n\n$$②$$ Решение: $$ \\overrightarrow{PA}=(x_1+5, y_1)$$ и $$ \\overrightarrow{PB}=(x_2+5, y_2)$$. \n$$ \\overrightarrow{PA} \\cdot \\overrightarrow{PB} = (x_1+5)(x_2+5) + y_1y_2 $$. \nТак как $$y_1=k(x_1+5)$$ и $$y_2=k(x_2+5)$$, то $$y_1y_2 = k^2(x_1+5)(x_2+5)$$. \n$$ \\overrightarrow{PA} \\cdot \\overrightarrow{PB} = (1+k^2)(x_1+5)(x_2+5) = (1+k^2)(x_1x_2 + 5(x_1+x_2) + 25) $$. \nПодставляя выражения из теоремы Виета: \n$$ = (1+k^2)\\left( \\frac{25k^2-9}{1+k^2} + 5\\left(-\\frac{10k^2}{1+k^2}\\right) + 25 \\right) $$ \n$$ = (1+k^2) \\frac{25k^2-9 - 50k^2 + 25(1+k^2)}{1+k^2} $$ \n$$ = 25k^2-9 - 50k^2 + 25 + 25k^2 = 16 $$.\n$$∴$$ Значение $$ \\overrightarrow{PA}\\cdot \\overrightarrow{PB}$$ равно $$16$$. (Это значение является степенью точки P относительно окружности C и не зависит от наклона секущей $$l$$).",
"qtype": "Задача с развернутым ответом",
"subject": "Математика/Аналитическая геометрия",
"grade": "Университет",
"has_img": false,
"image_analysis": {
"img0": {
"image_present": false
}
},
"classification": {
"major_category": "Science",
"sub_category": "Mathematics",
"subject": "Anal. Geom."
},
"correctness": {
"is_correct": true
},
"difficulty": {
"knowledge_point": "Уравнение геометрического места точек, Уравнение окружности, Уравнение прямой, Теорема Виета, Формула длины хорды, Скалярное произведение векторов, Степень точки относительно окружности",
"knowledge_level": "high school",
"educational_stage": "high school"
},
"quality": {
"logical_coherence": 5,
"educational_value": 4,
"clarity": 4
},
"question_metadata": {
"question_type": "Short Answer",
"language": "Russian",
"ai_generation_likelihood": 4
}
}
【真实性】题目来源可靠,题干、答案、解析、知识点、配图等信息完整
- 精选可靠题源: 题目均源自权威教材、认证习题集及机构内部讲义,保障内容根基。
- 智能分类赋能: 所有题目信息(题干、答案、解析、知识点、配图)均被完整结构化存储。核心亮点在于我们的
classification字段——它并非简单标签,而是经过大模型智能清洗初筛 + 人工专家抽样验证的精细化分级学科分类体系(一/二/三级)。这为 跨领域、高精准度 的题目筛选与应用奠定了坚实基础。 - 所有公式均以标准 LaTeX 格式封装,专业呈现,解析无忧。
{
"id": "dcb705347f19e67c20de8a97",
"title": "已知某金属离子$M^{n+}$与氨水反应形成配合物$[M(NH_3)_6]^{n+}$。若该配合物的磁矩为零,且金属离子的电子排布为$d^6$,试确定该金属离子在周期表中的位置,并说明理由。",
"option": null,
"answer": "铁",
"parse": "根据题目信息,金属离子的电子排布为$d^6$,并且形成的配合物磁矩为零,这意味着所有未成对电子都已配对。对于$d^6$电子排布,在八面体场中只有当形成低自旋态时,即所有电子都进入$t_{2g}$轨道并完全配对时,磁矩才会为零。因此,该金属离子应处于第VIII族,常见$d^6$电子排布且能形成低自旋态的金属离子是铁。铁在周期表中的位置为第四周期,第VIII族。",
"qtype": "简答题",
"subject": "化学/化学",
"grade": "大学",
"has_img": false,
"image_analysis": {
"img0": {
"image_present": false
}
},
"classification": {
"major_category": "Science",
"sub_category": "Chemistry",
"subject": "Inorg. Chem."
},
"correctness": {
"is_correct": true
},
"difficulty": {
"knowledge_point": "Coordination chemistry, Crystal field theory, Electronic configuration, Magnetic moment, Periodic table",
"knowledge_level": "high school",
"educational_stage": "university"
},
"quality": {
"logical_coherence": 4,
"educational_value": 4,
"clarity": 4
},
"question_metadata": {
"question_type": "Short Answer",
"language": "Chinese",
"ai_generation_likelihood": 4
}
}
【准确性】全量题库数据均完成去重清洗,统一格式,模型人工双重校验交叉审核
- 智能去重,题库纯净:采集完成后,基于深度语义相似度对全量题库进行 AI 级去重,从根源杜绝冗余题目。
- 统一架构,数据规范:所有题目均以严格定义的字段模型(id、学段、多级学科、题干、答案、解析等)进行标准化存储,奠定高质量数据基石。
- 核心防线,正确性的硬核质检: 答案与解析必须通过双重校验熔炉——先经 AI 模型初筛,再经人工专家复验。
correctness字段作为 最终裁决者,精准标识并强制剔除 所有 “问题题”:包括但不限于内容残缺、逻辑漏洞、数据异常或概念偏差等瑕疵样本,确保题库纯净度。
{
"id": "6807164f991513c1ae30f45a",
"title": "二氧化碳(CO_{2}$)的来源是以下哪一过程?",
"option": [
"A. 半水煤气经脱硫变换后的气体",
"B. 石灰窑燃烧产生的废气",
"C. 工业废气直接收集",
"D. 天然气直接燃烧"
],
"answer": "A",
"parse": "$侯氏联合制碱法通过将半水煤气进行脱硫和变换处理,获得含CO_{2}的变换气作为原料,这一过程既满足制碱需求,又解决了合成氨原料气脱碳的问题。B选项是索尔维法的CO_{2}$$来源,C选项未明确具体工业废气来源且不符合工艺描述,D选项天然气燃烧生成的CO_{2}$未提及脱硫等预处理步骤,均不符合题意。",
"qtype": "单选题",
"subject": "化学/工业化学",
"grade": "大学",
"has_img": false,
"image_analysis": {
"img0": {
"image_present": false
}
},
"classification": {
"major_category": "Engineering",
"sub_category": "Chemical Engineering and Technology",
"subject": "Mass Trans. & Sep. Process in Chem. Eng."
},
"correctness": {
"is_correct": false,
"error_type": "Wrong Answer"
},
"difficulty": {
"knowledge_point": "Industrial Chemistry, CO2 sources, Haber-Bosch process, Solvay process",
"knowledge_level": "high school",
"educational_stage": "university"
},
"quality": {
"logical_coherence": 3,
"educational_value": 4,
"clarity": 2
},
"question_metadata": {
"question_type": "Single Choice",
"language": "Chinese",
"ai_generation_likelihood": 4
}
}
【定制化】字段格式定制调整,细分学科细分语种题库定制采集
- 字段格式可以根据具体需求完成定制化调整、增添或删减等。
- 部分细分小众学科、小语种类的题库需求可定制化采集。
- 以 QA 对形式呈现的可用于 RL Verified 的构建。
- 测评筛选某些大模型高概率做错的题库数据集,赋能针对性训练提高。
{
"id": "67ff4799a366742fe5edf95b",
"title": "在泊松方程的九点差分格式中!!误差项 $R_{i,k}^*$ 的阶数为:",
"option": [
"A. $O(h^2)$",
"B. $O(h^4)$",
"C. $O(h^6)$",
"D. $O(h^8)$"
],
"answer": "C",
"parse": "根据九点差分格式的推导,误差项 $R_{i,k}^*$ 的估计式中包含 $h^6$ 的项,因此其阶数为 $O(h^6)$。",
"qtype": "单选题",
"subject": "数学/数值分析",
"grade": "大学",
"has_img": false,
"image_analysis": {
"img0": {
"image_present": false
}
},
"classification": {
"major_category": "Science",
"sub_category": "Mathematics",
"subject": "Num. Anal."
},
"correctness": {
"is_correct": true
},
"difficulty": {
"knowledge_point": "Poisson equation, nine-point difference scheme, error term, order of accuracy, numerical analysis",
"knowledge_level": "university",
"educational_stage": "university"
},
"quality": {
"logical_coherence": 4,
"educational_value": 3,
"clarity": 4
},
"question_metadata": {
"question_type": "Single Choice",
"language": "Chinese",
"ai_generation_likelihood": 4
}
}
【AI4S】题库之外,知识之海
- 整数智能也提供大量 论文、教材 等 非题库 类 AI4S(AI for Science)数据。
- 垂直领域类专家模型需要论文、教材等特殊的数据类型,这类数据数量相较于题库类数据来说极其稀少。
- 整数在题库数据集之外,还构建了论文和教材两大数据库,共同覆盖 AI4S 的各类数据需求。
整数智能信息技术(杭州)有限责任公司,起源自浙江大学计算机创新技术研究院,致力于成为AI行业的数据合伙人。整数智能也是中国人工智能产业发展联盟、ASAM协会、浙江省人工智能产业技术联盟成员,其提供的智能数据工程平台(MolarData Platform)与数据集构建服务(ACE Service),满足了智能驾驶、AIGC等数十个人工智能应用场景对于先进的智能标注工具以及高质量数据的需求。

目前公司已合作海内外顶级科技公司与科研机构客户1000余家,拥有知识产权数十项,通过ISO9001、ISO27001等国际认证,也多次参与人工智能领域的标准与白皮书撰写,也受到《CCTV财经频道》《新锐杭商》《浙江卫视》《苏州卫视》等多家新闻媒体报道。



 浙公网安备33010902003900
浙公网安备33010902003900