o1之后：Lean 4数学形式化证明推动AI Reasoning下一次飞跃

1. 引言

OpenAI o1模型以其卓越的推理能力引起了无数关注。在推理能力和思考能力上，o1超越了以前的模型（尤其是Science和Coding等任务上）。在处理复杂任务时展现出的出色表现，激发了人们对模型推理能力的深入探讨。此外，随着科技的深入发展，许多领域都依赖于复杂的数学算法和精确的逻辑推理。例如，在金融、工程、物理和计算机科学等领域，问题的复杂性和规模不断增长，如何提升AI的推理能力已成为亟待解决的挑战。

2. 推理能力的前沿：数学形式化证明

2.1. 为什么我们需要模型的推理能力

数学和逻辑推理作为科学和工程的基础，它们在解决复杂问题时发挥着关键作用。大模型通过增强的推理能力，可以更好地模拟人类解决问题的方式，从而在科学研究、工程设计、医疗诊断、金融分析等领域提供更深入的见解和更准确的决策支持。此外，随着数据量的爆炸性增长，我们需要更智能的系统来处理和分析这些数据，而具备推理能力的大模型正是实现这一目标的关键工具，我们期待模型能实现：

复杂问题的求解：现代科学和工程问题的复杂度超出了传统方法的承受范围，大模型的引入能够处理和解决这些复杂的问题。
提高效率和准确性：大模型通过自动化推理和计算，可以大幅提高复杂任务的处理效率，并减少人为错误。
创新和发现：大模型凭借其强大的推理能力，可以在未知领域进行探索和创新，发现新的理论和规律。

OpenAI o1以其在复杂任务中展现出的推理能力，点燃了行业对于模型推理能力的研发热潮。然而，如何进一步提升这一能力，成为了AI研究者们面临的挑战。将数学形式化证明（Formal Verification）融入AI大模型的训练，无疑是提升其推理能力的有效路径。

2.2. 什么是形式化证明

在数学体系的搭建过程中，证明显现出其不可或缺的地位。数学研究的根本任务是探索数学对象的性质、关系和结构，而这一切都依赖于严密的逻辑推理。证明在数学中不仅是一种结果的呈现，在现代数学的背景下，证明作为数学研究的核心，承担着探索与验证的双重角色。随着研究对象的复杂性和理论体系的日益庞大，证明的规范性要求显著提高，传统的非形式化证明虽然在历史上起到了重要的推动作用，但在面对日益复杂的数学概念时，常常无法满足严谨性和准确性的要求。形式化证明相较于非形式化证明，具有以下优点：形式化证明则通过严格的逻辑和明确的表达避免了这些问题，确保了推理过程的精确性和可靠性。

形式化证明的核心在于使用严格的公理体系、定理和推理规则，以确保每一步推理的严密性和准确性。形式化证明为数学家提供了一种精确的表达工具，使得每一个逻辑推理都能够在一个公认的框架内进行，每个概念和操作都有明确定义，例如，形式化的公理系统能够严格界定各种数学对象及其关系。形式化证明还通过使用公理、定理和推理规则，提供了一种系统化的方法来验证数学命题的正确性。具备相关背景知识的人可以通过形式化的描述，独立地检查和验证证明的每个步骤，确保了数学理论的正确性与可重复性，不仅对证明规范性要求做出回应，更能推动数学研究向更高层次发展。这种透明性不仅有助于建立数学界的信任，还促进了知识的传播与传承。通过使用一致的逻辑语言和符号，研究人员能够在不同的数学领域和应用之间建立联系，使得理论的推广和应用更加顺利。

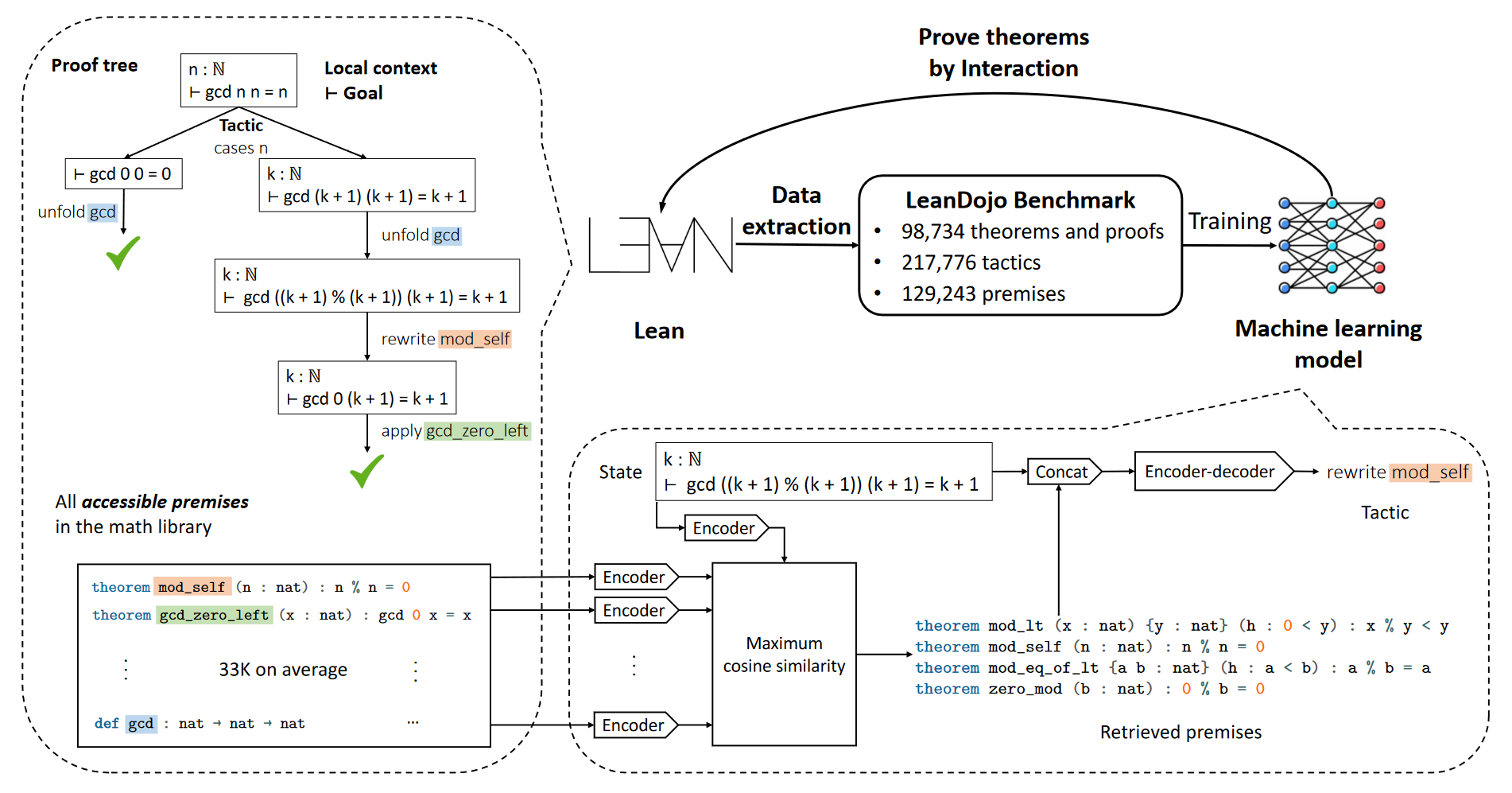
Yang et al. (2023). LeanDojo: Theorem Proving with Retrieval-Augmented Language Models. arXiv:2306.15626.

3. Lean 4：数学形式化证明的利器

Lean是一种编程语言，可以作为定理证明时的辅助证明工具。 它提供了一个严格的逻辑和数学框架，支持高阶逻辑和依赖类型理论，使得用户可以高效的进行精确的推理和证明，其交互式证明环境允许用户逐步构建证明并实时检查其正确性，它提供的即时反馈大大降低了用户的调试成本。此外，Lean支持模块化编程，允许用户将证明和定义组织成模块。便于重用和管理，使得大型项目的开发更加高效和清晰。总之，Lean为研究人员提供了一个可靠的工具，用于验证新理论和结果的有效性，确保研究过程中的严谨性和可重复性，这种集成的形式化证明工具为学术界提供了新的视角，助力推动更高水平的数学和科学发现。

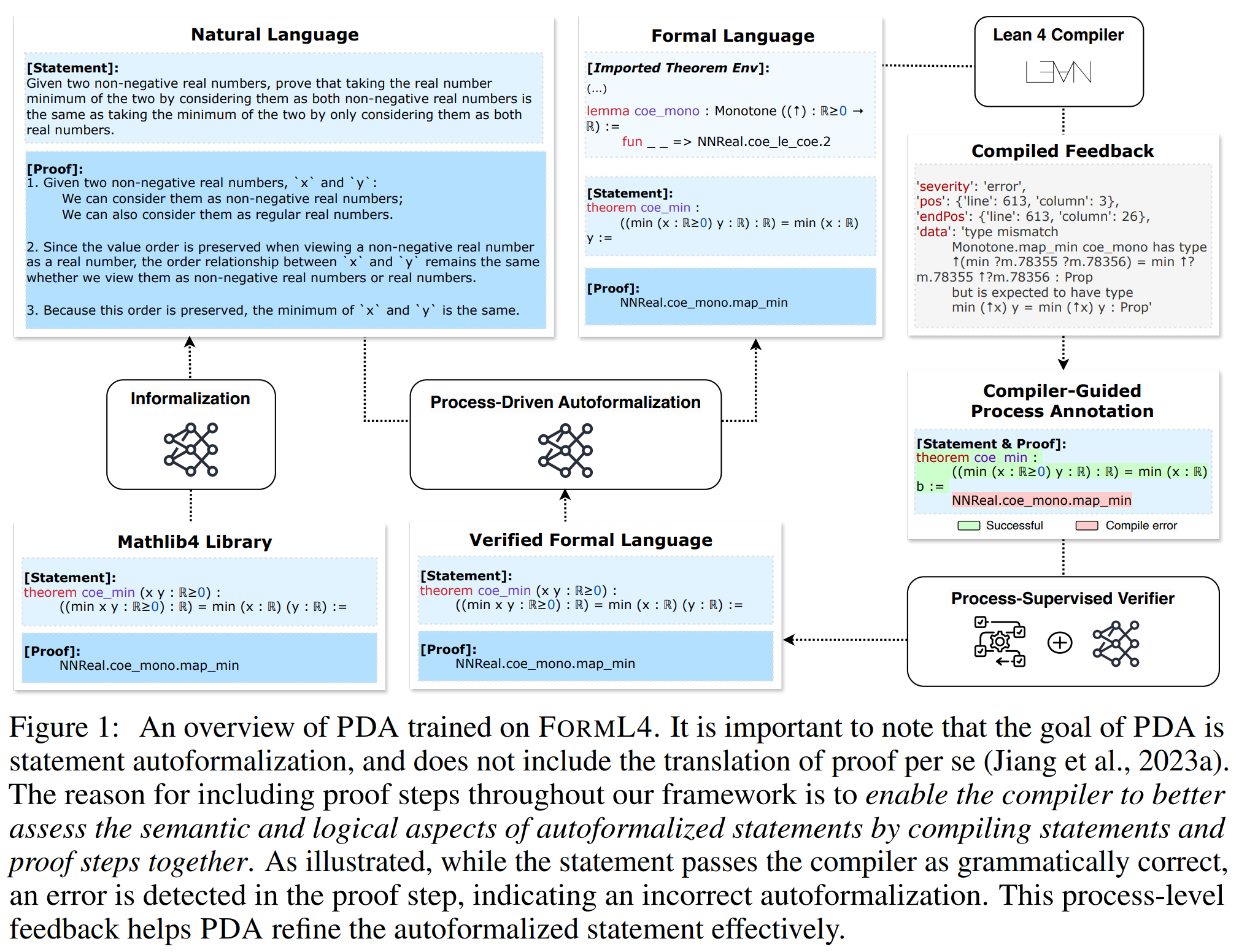
Lu et al. (2024). Process-Driven Autoformalization in Lean 4. arXiv:2406.01940.

4. 我们正在做什么

整数智能的团队利用Lean 4的能力，正在着力打造形式化证明数学语料库，为推理大模型的数学训练提供高质量的数据集，增强其在数学推理领域的表现。我们相信，这是一件在当下和未来都极具价值和潜力的事情。

4.1. 构建Lean 4数据集的挑战

4.1.1. 自然语言的模糊性

在处理存在于数学与科学领域的由自然语言表述的命题时，Lean 4面临着严峻的挑战，这些问题通常表现为模糊、缺乏精确性或包含隐含的假设，使得它们难以直接转换为形式化的证明。在自然语言中，部分命题使用诸如“所有”、“某些”或“大多数”等量化词汇，这些词汇在数学中具有特定的含义，但在自然语言的语境中可能模糊不清，这意味着它隐含了许多未明确说明的假设和条件，需要引入额外的定义和条件，使得逻辑推理更加复杂。这意味着，在解释一个命题时，往往需要依赖于对上下文或特定背景知识的精确提取，确保所有的定义和隐含假设都得到明确化。此外，对于需要证明的内容不明确表述的题目，Lean 4无法直接识别证明的目标。例如，疑问形式的表述往往包含开放性和不确定性，一个问题如“这个数列的极限是多少？”不仅没有明确的数列定义，也未提供相关的条件和背景信息，这与Lean 4所需的精确性和封闭性相悖。因此，为了使得这些问题能够被Lean 4处理，必须首先将其转换为具体的陈述形式，并明确所有相关的条件和定义，只有这样，Lean 4才能进行有效的推理和证明。

4.1.2. 专业领域知识的要求

由于Lean 4所处理的数学和科学命题往往涉及高度专业化的领域，这意味着即使是资深的数学家，也可能无法轻松处理每一个命题的形式化证明。数学工作的分领域特性使得一个研究者可能精通特定领域，但在其他领域知识储备有限。因此，在构建Lean 4数据集时，确保不同领域的专家共同参与显得尤为重要。

4.1.3. 流程管理的复杂性

在构建Lean 4数据集的过程中，流程管理的复杂性与对参与者主观能动性的依赖也是一大挑战。在大规模的数据生产中，我们不能假设每个人都能保持高效的工作态度、严格的认真精神。同时，由于审核动作相对较少，存在着一定的投机空间。

有效的流程管理至关重要，但实现这种管理尤其复杂。构建大规模的数据集要求多个人员和多步骤的协作，每个环节都可能出现问题，导致整体效率和数据质量的下降。例如，某些参与者可能在数据处理、转换和验证过程中因为工作态度不积极或审查不严格，导致产生低质量的数据。这不仅影响了Lean 4的推理和证明效果，更可能在后续的研究和应用中带来隐患。

4.2. 我们的解决方案

4.2.1 建立精确的命题解析流程，完善的审核机制

我们与广大高校的数学和科学领域的专家建立了合作关系，组织跨学科团队，建立专家数据库，涵盖数学各分支和相关科学领域，方便快速匹配项目需求，邀请对应领域的专家参与命题的解析和证明工作。由专业数学工作者组成的团队制定严格的标准，对自然语言命题进行深入解析，检测命题中的模糊词汇，明确所有定义、符号和隐含假设，将对常见的量化词汇（如“所有”“某些”“大多数”等）制定统一的标准解释。我们使用先进的协同工具，管理任务分配、进度跟踪和沟通交流，及时收集参与者的反馈，调整流程和策略，持续优化，建立了即时反馈机制，确保命题解析结果经过建议团队的严格审核。

4.2.2. 高校项目资源与专有领域数据库

在专业领域知识的支持方面，我们的方案不仅依赖内部的知识体系构建，还通过与高校的精准合作，充分利用外部专家资源，确保数据集的高质量。在题目和命题的选择上，我们采用严格的精挑细选流程，以确保每个题目都符合Lean 4的处理能力边界。我们选择的题目不仅要求具备逻辑清晰性和封闭性，还确保其在数学和科学领域具有足够的研究价值和验证意义。我们在题目选择阶段设置了多层次的评估流程，首先由内部专家对题目进行学术价值、技术难度等方面的筛选，确保入库题目在学术性、创新性和Lean 4适用性上均达到标准。我们设计了一套难度评估体系，对每个命题的证明复杂性进行分级。根据客户的模型训练需求，我们可以提供定制化的数据，使数据集在初级、中级或高级难度范围内均衡，确保数据集在指定领域内具有足够的覆盖度，以增强模型在该领域的表现满足不同训练阶段的需要。

4.2.3. 严格的分步流程与审核机制

我们设计了全面的管理与质量控制方案，数据生产人员需通过一系列专业资格认证和考核，包括数学基础知识、Lean 4使用能力和数据处理经验等方面的评估，使用自动化的任务分配系统，根据参与者的资质和经验，动态分配任务，以确保每一环节的参与者能够高效地执行相应工作。针对每位数据生产人员的工作质量，我们设置了责任追踪系统，识别出潜在的低效行为，并根据反馈实时改进，帮助提升整体生产水平，确保数据集的稳定高质。

4.3. 如何利用Lean 4进行数学标注

整数智能的高水平标注团队通过精确的数学符号和表达，依据Lean4语言规则，为数学命题增加注释，将其变为Lean 4能够识别的形式，严格按照公理体系、定理和推理规则，确保形式化证明每一步推理的严密性和准确性。

我们的工作流程包括以下几个步骤：

数学命题的选择与分析：我们从广泛的数学领域中选择具有代表性和挑战性的命题，进行深入分析。筛选过程中，团队不仅评估命题的逻辑严谨性，还结合客户的模型需求选择合适的知识覆盖范围和难度等级，以确保数据集对不同训练需求的适用性，确保其适合进行形式化证明。
形式化证明的构建：团队根据Lean 4规则为数学符号和表达添加详细注释，保证每一步的形式化过程在Lean 4中可识别，增强推理的清晰度和严谨性。确保每一步推理都符合数学逻辑和Lean 4的规则。
数据集的整理与优化：我们将这些形式化证明整理成数据集，保证数据集在结构、格式和符号使用上的一致性，便于模型训练和学习。通过流程管理和质量审查，对数据集进行优化和验证，确保数据集的质量和可用性。
数据集的应用与反馈：我们的数据集被应用于各种推理大模型的训练中，我们与数据应用方保持紧密联系，收集模型在实际应用中的反馈，快速调整数据集，优化证明结构、难度范围和知识覆盖，确保数据集在未来的应用中始终保持领先优势。结合行业需求和模型反馈，数据集定期更新扩展，以覆盖更多领域的知识，为模型提供更全面的训练数据。

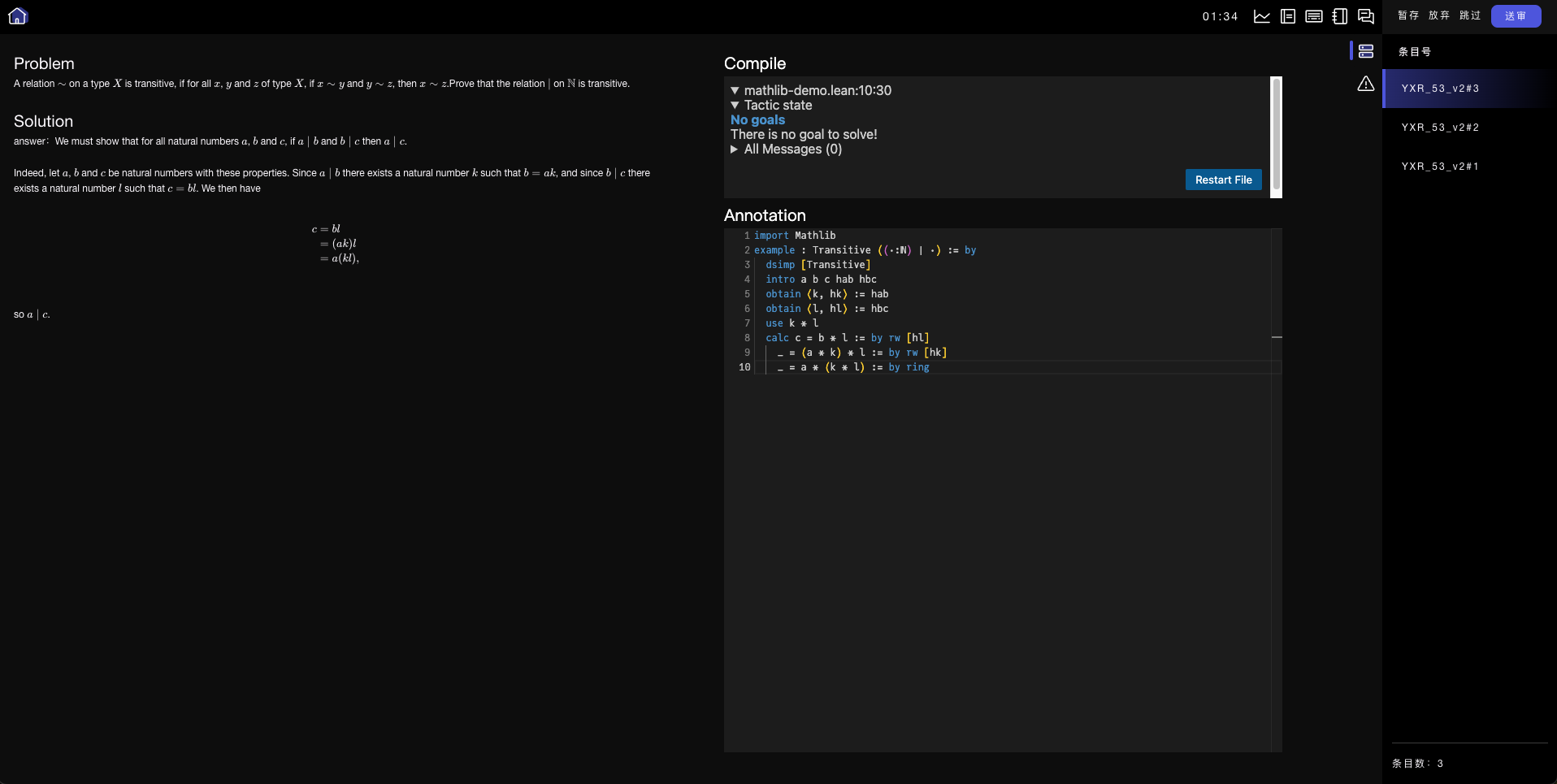
整数家MooreData智能数据工程平台标注界面

4.4. 整数家的数学数据集解决方案优势

相比于市面上的其他数据集，整数智能的数学数据集具有以下优势：

广泛的数学分支覆盖：我们的数据集覆盖了多个数学分支，包括但不限于代数、几何、数论和分析学，能够应对更多场景下的数学问题。
丰富的题型与应用场景：我们的数据集不仅包括规范化的数学命题，还涵盖了许多应用场景或生活场景下的非规范化问题，如生活场景中的数学推理题和自然语言形式的应用问题，涵盖了金融计算、工程应用等实际场景，使模型能更好地理解数学在不同应用场合的具体需求，提升模型在跨领域应用中的表现。
高级逻辑结构的丰富性：我们的数据集包含了大量的高级逻辑结构，我们引入了复杂的逻辑结构，诸如嵌套推理、多步证明、条件分析等，这些结构对数学证明流程的体现更接近本质，数据集中的每一步推理都经过严谨的设计和注释，确保模型在学习过程中能够清晰地掌握每一逻辑步骤。通过系统性地理解并应用这些逻辑结构，模型在处理复杂证明任务时能够展现出更强的逻辑严谨性和高效性。
数据质量和专业性保证：相比于市面上其他数据集，我们的数据集在数学知识深度和数据标准化方面更具优势。基于客户的不同需求，我们的数据集能够在题型、难度、领域覆盖等方面灵活定制，确保模型训练能够精准匹配特定的应用需求，助力客户在高精度、广泛适用的模型应用中取得更佳成效。

5. 整数家的思考

数学在人类文明的发展中有着悠久的历史，并扮演着不可替代的核心角色。它不仅是一种探索世界本质的语言，也是一门支撑多学科发展的基础科学。它通过揭示和探索隐藏在世界现象背后的抽象规律和逻辑结构，不仅提供了描述现实世界的语言和工具，还通过其严谨的推理和精确的表达，保障了各种科学理论的正确性和自洽性，展现出独特的力量和广泛的应用价值。

数学的定义随时间演变，反映了研究内容的扩展和认识的深化。在古代文明中，数学主要关注数量（算术）和空间（几何），用于天文、农业和建筑等领域。这一时期，数学从简单的计算发展到了定理推导。

进入近代（17世纪至19世纪），数学变得更加抽象和系统化，不再仅限于解决具体问题。代数开始探索更深层次的结构，微积分的发明使得研究变化成为可能。这一阶段标志着数学向高度抽象化与逻辑化的转变，并形成了多个相互联系但独立发展的领域。

到了现代，尤其是20世纪以后，数学进一步抽象化、系统化，并广泛应用于各个领域。集合论成为了现代数学的基础之一，促进了数学对象的形式化处理。同时，不同数学分支之间也展现出更高的内在统一性，使得对抽象概念的研究更加深入且系统化。简而言之，数学从最初的实用工具逐渐演变成了一门探索自然界普遍规律的科学。

尽管形式化证明在现代数学研究中已经表现出明显的优势，且在提升数学研究的准确性和严谨性方面展现了巨大潜力，其发展依旧面临一些挑战。首当其冲的是学习曲线陡峭的问题，形式化证明要求将复杂的数学概念以严谨的符号和逻辑语言表达。这种表达方式虽然消除了模糊性，但在某些情况下，可能会使得数学思维变得更加繁琐和复杂，特别是对于一些高层次的抽象概念，形式化表达的过程可能变得极其复杂和冗长，增加了理解和沟通的难度。形式化证明虽然具备更高的可验证性，但也意味着每一个细节都需要仔细审查和确认，特别是在处理复杂的数学结构时，研究者需要付出额外的努力来确保每个步骤都是正确的。推动形式化证明的生成和验证的高效化与便捷性不仅是应对现代数学研究复杂性和实际应用需求的必然选择，也是提高研究效率、确保结果可靠性和促进教育发展的重要手段。引入自动化和交互式定理证明工具成为一种策略。

形式化证明工具的发展反映了数学与计算机科学交融的深刻变革。形式化证明工具的发展历程可以追溯到20世纪中叶，早期的自动定理证明器，如Resolution Principle和Herbrand’s Theorem的引入，为形式化证明奠定了基础。在1970年代至1980年代，形式化方法（Formal Methods）迅速发展，多个重要的定理证明工具相继问世。例如，Coq（1989）和Isabelle（1986）等工具开始流行，它们支持交互式证明，允许用户以更自然的方式构建证明。1990年代，丰富的库与工具蓬勃发展，Coq的Mathematical Components库在数论和代数中得到广泛应用，结合高阶逻辑与交互式证明的Isabelle/HOL则应用于形式化验证和安全性分析。2000年代至今，依赖类型理论在形式化证明中的应用不断增加。依赖类型理论（Dependent Type Theory）是一种将类型与值紧密结合的类型系统，它的核心思想是允许类型依赖于某些值。通过依赖类型，形式化证明可以允许用户定义更复杂的结构和函数，更加精确地定义数学对象及其属性，通过类型表达复杂的逻辑关系，此外，依赖类型理论允许在编译时进行类型检查，这就意味着形式化证明的正确性可以在代码级别上得到验证。

Lean 4的优势在于其高效的证明能力和强大的库支持。它支持模块化编程，允许用户将证明和定义组织成模块，便于重用和管理。此外，Lean 4的交互式证明环境允许用户逐步构建证明并实时检查其正确性。然而，Lean 4也存在一些挑战，例如在处理复杂的数学问题时，自动推理能力有限，依赖于用户提供的提示和结构。

Lean 4在形式化证明领域展现出显著的优势，但在效率上仍有很大改善空间。首先，Lean 4的自动推理能力在处理复杂的数学问题时，仍然依赖于用户提供的提示和结构，这在一定程度上限制了其自动化的程度。尽管Lean 4拥有丰富的数学库，但在特定领域的知识和定理的覆盖上，仍有不足之处。某些特定的数学分支或新兴领域的定理可能尚未被充分形式化，导致自动证明的能力受限。这意味着在面对高度复杂或不规范的命题时，Lean 4可能无法生成有效的证明，而需要更多的人工干预和指导。

6. 结语

在AI推理能力的探索之路上，数学形式化证明正成为一把越来越重要的钥匙。通过将这一概念融入大模型的训练，我们能够显著提升模型的推理能力。整数智能的高质量的数学数据集不仅涵盖了广泛的数学分支，还包括了丰富的题型和高级逻辑结构，为模型提供了全面的学习材料。使推理大模型能够更好地理解和处理复杂的数学问题，从而在各个领域中发挥更大的作用。